Contents:
Detection Theory: MAP, LRT, Minimum Error Test, Error Probability.
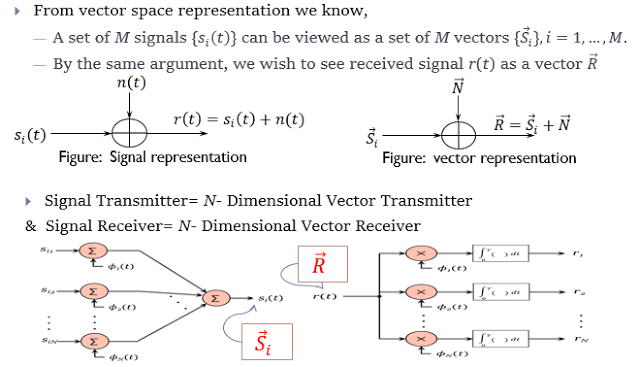
Signal space representation :
- Geometric representation of signal
- Continuous AWGN channel as a vector channel,
Likelihood functions, Coherent Detection of binary signals in presence of noise, Optimum Filter,Matched Filter, Probability of Error of Matched Filter, Correlation receiver.
Detection Theory:
- Synonyms
- Detection
- Decision Making
- Hypothesis Testing
- Decoding
Detection:
To decide whether some phenomenon is present or not based on the some observations.
Making:
process of deciding between a number of mutually exclusive alternatives.
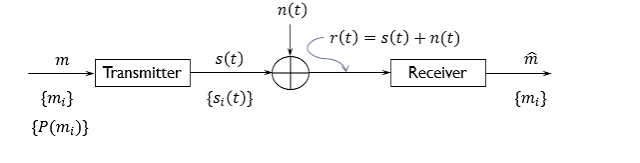
The process of mapping the received signal into one of the possible set of codewords/ transmitted symbols
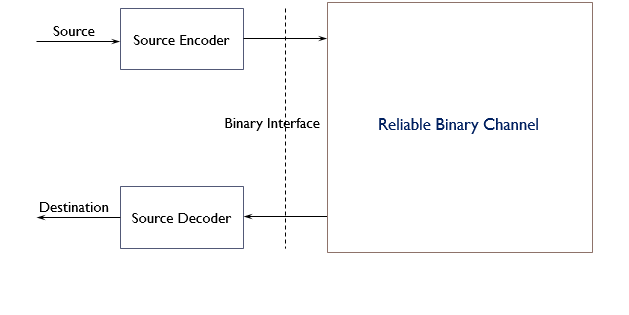
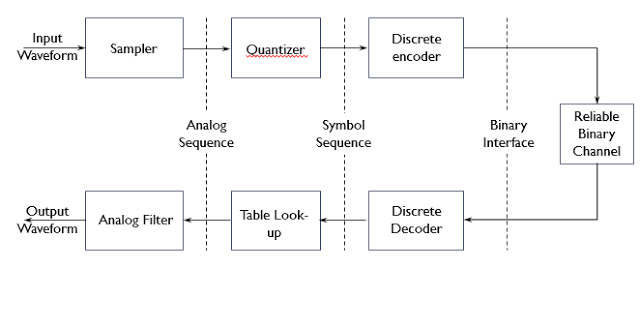
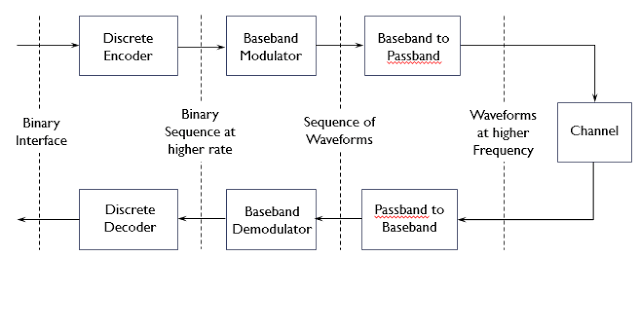
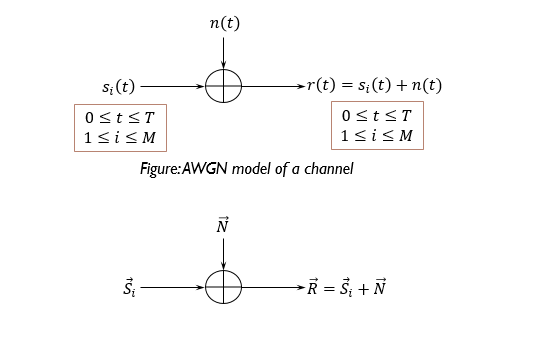
Additive white Gaussian noise (AWGN) is a basic noise model used in Information theory to mimic the effect of many random processes that occur in nature. The modifiers denote specific characteristics:
Additive because it is added to any noise that might be intrinsic to the information system.
White refers to the idea that it has uniform power across the frequency band for the information system. It is an analogy to the color white which has uniform emissions at all frequencies in the visible spectrum.
Gaussian because it has a normal distribution in the time domain with an average time domain value of zero.
Wideband noise comes from many natural sources, such as the thermal vibrations of atoms in conductors (referred to as thermal noise or Johnson-Nyquist noise), shot noise, black body radiation from the earth and other warm objects, and from celestial sources such as the Sun. The central limit theorem of probability theory indicates that the summation of many random processes will tend to have distribution called Gaussian or Normal.
AWGN is often used as a channel model in which the only impairment to communication is a linear addition of wideband or white noise with a constant spectral density (expressed as watts per hertz of bandwidth) and a Gaussian distribution of amplitude. The model does not account for fading, frequency selectivity, interference, nonlinearity or dispersion. However, it produces simple and tractable mathematical models which are useful for gaining insight into the underlying behavior of a system before these other phenomena are considered.
A basic and generally accepted model for thermal noise in communication channels, is the set of assumptions that
the noise is additive, i.e., the received signal equals the transmit signal plus some noise, where the noise is statisticaly independent of the signal.
The noise is white, That is, the power spectral density is flat, so the autocorrelation of the noise in time domain is zero for any non-zero time offset the noise samples have a Gaussian distribution.
Mostly it is also assumed that the channel is Linear and Time Invariant. The most basic results further asume that it is also frequency non-selective.
y = awgn(x,snr)
y = awgn(x,snr,sigpower)
y = awgn(x,snr, ‘measured’)
y = awgn(x,snr, sigpower,s)
y = awgn(x,snr,’measured’,state)
y = awgn(…,powertype)
The commands below add white Gaussian noise to sawtooth signal. It then plots the original and noisy signals in Matlab
t = 0:.1:10;
x = sawtooth(t); % Create sawtooth signal.
y = awgn(x,10,’measured’); % Add white Gaussian noise.
plot(t,x,t,y) % Plot both signals.
legend(‘Original signal’,’Signal with AWGN’);


Conversion of AWGN Channel into a Vector Channel: